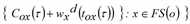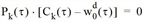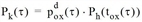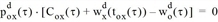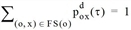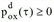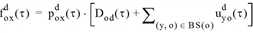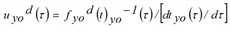In diesem Abschnitt wird der Ansatz für die dynamische Netzbelastungsfunktion mit einer impliziten Wegeaufzählung im Fall eines deterministischen Routenwahlmodells erklärt. Zu diesem Zweck wird zunächst das kontinuierliche dynamische Kurzwegproblem definiert, das dem Routenwahlmodell zugrunde liegt.
Kontinuierliches dynamisches Kurzwegproblem
Im Gegensatz zum statischen Fall schließt das Kurzwegproblem die zeitliche Dimension im dynamischen Kontext explizit ein, da die Kosten der Kanten, die einen Weg bilden, zu unterschiedlichen Zeitpunkten ausgewertet werden, übereinstimmend mit den Fahrzeiten auf der Kante, bedingt durch die rekursive Gleichung [29]. Danach werden die minimalen Kosten wod(τ) zwischen jedem Knoten o∈N und einem vorgegebenen Ziel d∈Z für Nutzer ermittelt, die zum Zeitpunkt t abfahren.
wod(τ) = min{Ck(τ): k ∈ Kod} [49]
Es kann bewiesen werden, dass die folgende dynamische Variante der Bellman-Relation für jeden Knoten o∈N (Abbildung 131) dem Problem [49] entspricht.
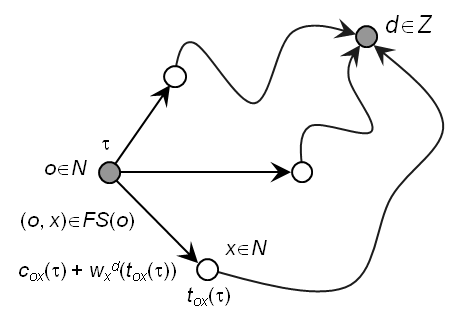
Abbildung 131: Dynamische Variante der Bellman-Relation
Die Bellman-Relationen [50] können durch einen dynamischen Programmieransatz gelöst werden, der nachfolgend beschrieben wird.
Wegewahl- und Flusspropagierungsmodelle
Wird davon ausgegangen, dass Verkehrsteilnehmer perfekt informierte rationale Entscheidungsträger sind, dann wählen sie ausschließlich die kürzesten Wege. Das deterministische Routenwahlmodell für Nutzer, die zum Zeitpunkt t von Quelle o∈N zu Ziel d∈Z fahren, kann dann mit folgender dynamischer Erweiterung des Wardrop’schen ersten Prinzips Folgendes formuliert werden:
- Wird Weg k ∈ Kod genutzt, das heißt seine Wahlwahrscheinlichkeit Pk(τ) ist positiv, dann sind dessen Kosten Ck(τ) genauso hoch wie die minimalen Kosten wod(τ), um zum Zeitpunkt t von o nach d zu fahren.
- Wird Weg k umgekehrt nicht genutzt, das heißt seine Wahlwahrscheinlichkeit ist null, dann dürfen dessen Kosten nicht kleiner sein als die minimalen Kosten.
Dies kann formal wie folgt ausgedrückt werden.
Darüber hinaus müssen die Wahlwahrscheinlichkeiten nicht negativ sein und in der Summe 1 betragen.
Im Folgenden wird eine Gleichung entwickelt, die für Routenwahl und Flusspropagierung auf einer impliziten Wegeaufzählung basiert und den Zeitscheibenansatz anwendet, bei dem die Abflusszeit vom aktuellen Knoten den zeitlichen Rahmen bildet.
Laufen die zum Zeitpunkt t von Verkehrsteilnehmern genutzten Kurzwege von o∈N nach d∈Z über mehr als eine ausgehende Kante eines Zwischenknotens x, dann könnten die bedingten Wahrscheinlichkeiten dieser Kanten zum Zeitpunkt t für nach d fahrende Nutzer theoretisch von den zwischen o und x genutzten Teilwegen abhängen. Aufgrund der additiven Kantenkosten wird aber stattdessen davon ausgegangen, dass die bedingten Wahrscheinlichkeiten der Kanten an jedem Knoten für alle Verkehrsteilnehmer gleich ist, die zum gleichen Ziel fahren, unabhängig von den bisher genutzten Teilwegen.
Unter dieser Annahme entspricht die Wahlwahrscheinlichkeit Pk(τ) eines Wegs k ∈ Kod von o∈N nach d∈Z für Nutzer, die zum Zeitpunkt t abfahren, dem Produkt der bedingten Wahrscheinlichkeiten seiner Kanten A(k), wovon jede auf den Zeitpunkt verweist, zu dem die Nutzer die Kante erreichen. Die Wahlwahrscheinlichkeit von k kann dann aus der nachfolgenden rekursiven Gleichung gewonnen werden.
Dabei ist (o, x) die erste Kante von k und h ∈ Kxd der Rest des Wegs k.
Die dynamische Wardrop-Bedingung ist erfüllt, wenn die bedingten Wahrscheinlichkeiten der Kanten wie folgt berechnet werden.
Gleichung [49] besagt, dass Verkehrsteilnehmer, die Knoten o∈N zum Zeitpunkt t verlassen und zum Ziel d∈Z fahren, unter den ausgehenden Kanten FS(o) nur eine Kante (o, x) auswählen können, für die die Summe aus den Kantenkosten Cox(τ) und der der minimalen Kosten wxd(tox(τ)) für den Restweg zum Ziel den minimalen Kosten wod(τ) entspricht. Die Durchfahrtszeit in x ist dabei tox(τ).
Der Fluss foxd(τ) der Fahrzeuge, die zum Ziel d∈Z fahren und die Kante (o, x)∈A zum Zeitpunkt t befahren, ergibt sich aus der bedingten Wahrscheinlichkeit poxd(τ) der Kanten multipliziert mit dem Fluss, der Knoten o zum Zeitpunkt t verlässt. Dieser ergibt sich wiederum aus der Summe des Abflusses uyod(τ) aus jeder Kante (y, o)∈BS(o), der in o einfließt, und aus der Nachfrage Dod(τ) von o nach d. Damit ergibt sich folgende Gleichung:
Werden die FIFO- und Flusserhaltungsregeln angewandt, kann der Abfluss von y zum Zeitpunkt τ anhand des Zuflusses zu a zum Zeitpunkt tyo-1(τ) so ausgedrückt werden.
Dabei beruht das Gewicht dtyo(τ)/dτ auf der Tatsache, dass Fahrzeiten zeitlich variieren und die Abflussrate einer Kante kleiner ist als die Zuflussrate, falls die Reisezeit zunimmt (und umgekehrt).
Der gesamte Zufluss und Abfluss der Kante (o, x)∈A zum Zeitpunkt t ist dann folgendermaßen: